此笔记仅作本人学习、复习与思考用。
堆:是一个完全二叉树,该数据结构遵循一个规则,根节点大小必须大于或者小于孩子节点的大小。
堆排序:利用堆结构的特性来进行排序,比如,假设有数集Z={x1,x2,x3,…,xn},该数集初始是一个无序序列,现在通过堆排序对其进行排序,首先将该序列调整成堆,即满足堆定义的序列,其次将堆顶(建堆完成之后,堆顶就是该数集的最大值)与末元素进行对换,然后将该数集变成Z={x1,x2,x3,…,xn-1},直到Z={x1},则排序完成。
核心步骤:建堆过程
建堆过程:首先这是一个从下到上,从右到左的调整过程。
1,从该完全二叉树的最下最右的子树进行调整(比较懒,直接搬运别人的图)
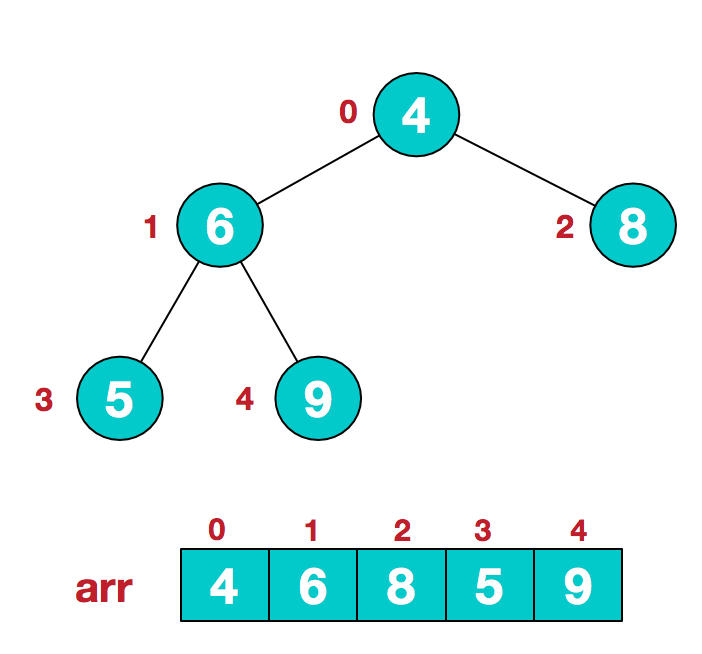
调整 比较1,3,4 这三个的大小,然后做出调整,比较的过程是先比较孩子大小,再让孩子比较根的大小,调整完毕之后就变成这样子
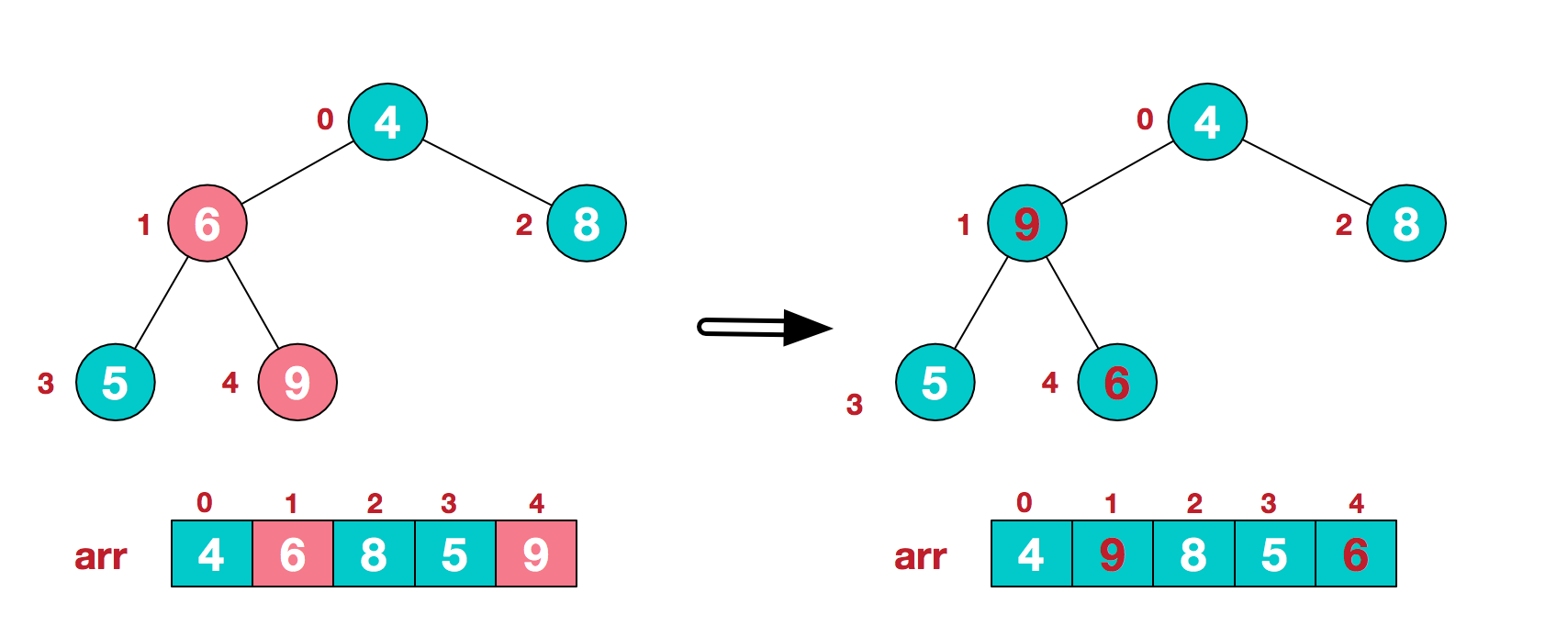
2,继续左移根节点即第一次调整的树1,现在调整树0,调整步骤同上,调整完成之后
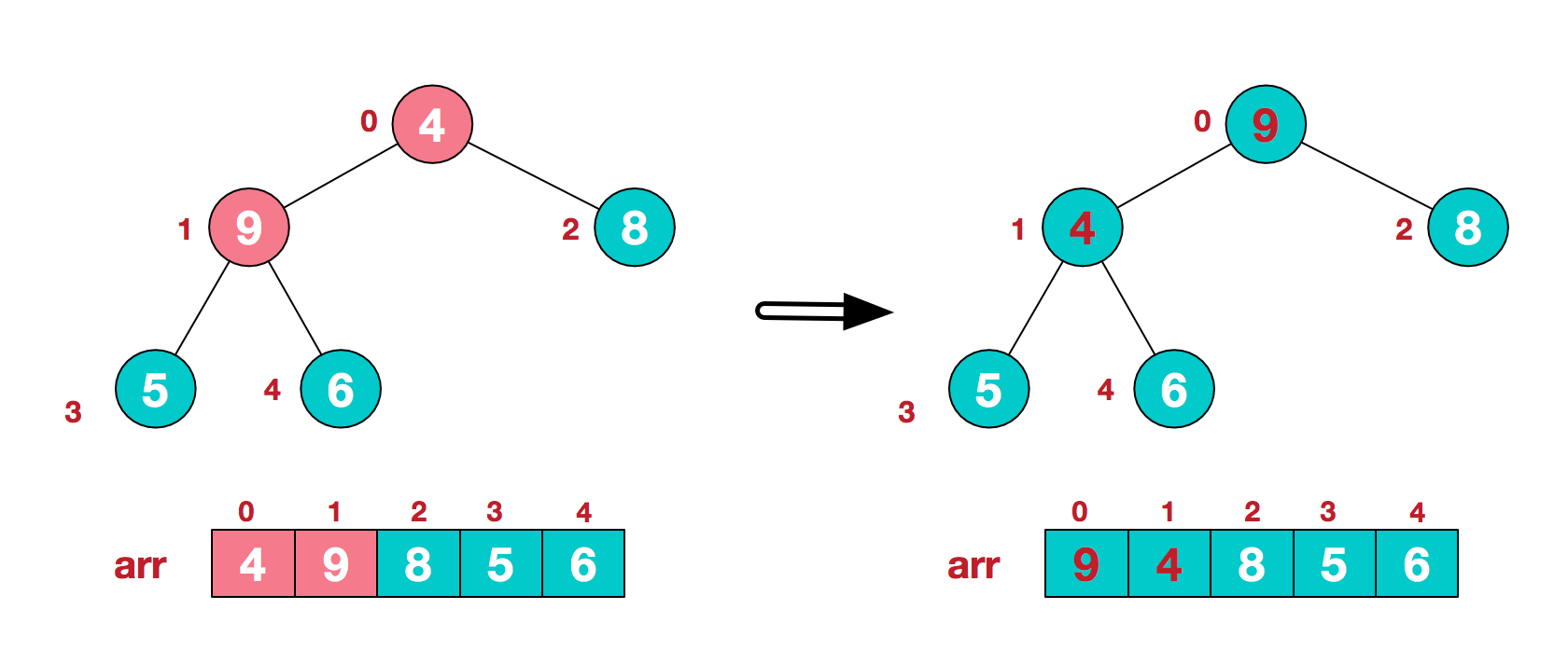
但是会发现,这样调整之后,树1就不满足堆定义,需要重新调整树1,所以最后调整的结果是
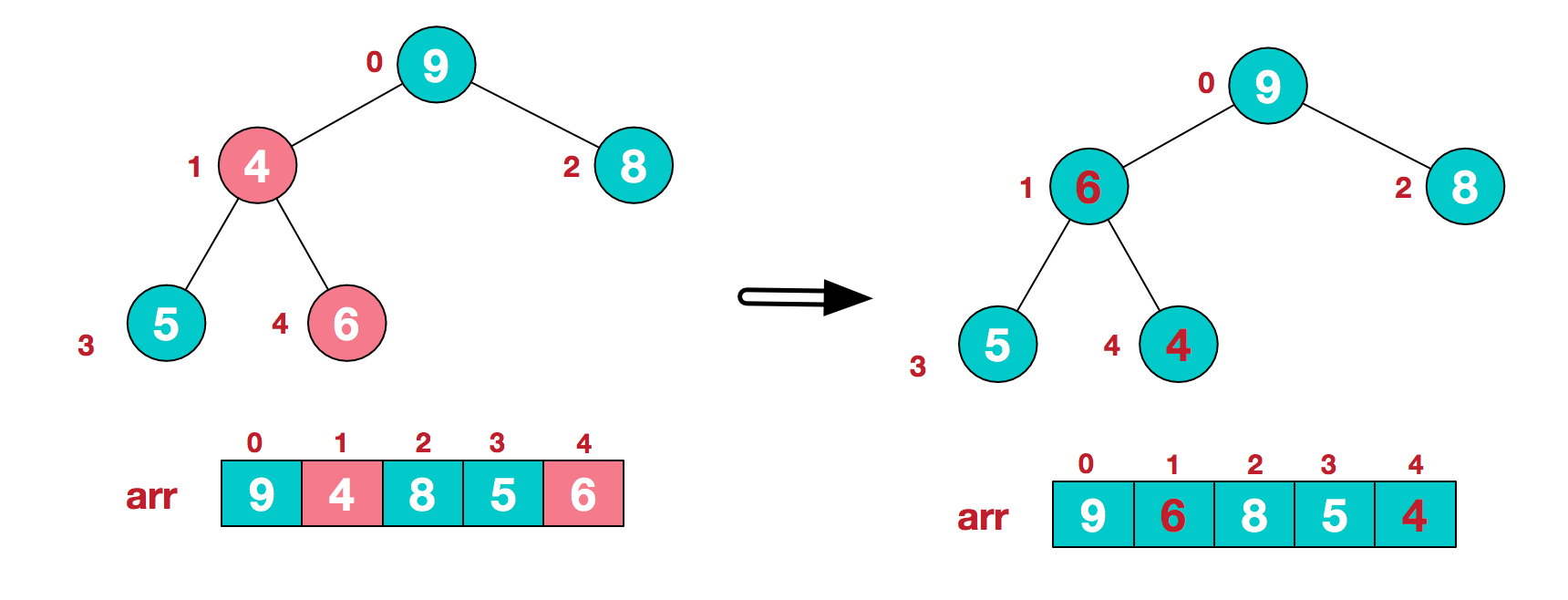
此时建堆过程结束,就进入首尾调换元素的步骤。该算法的核心步骤就是建堆,所以图示就只介绍到建堆完毕。
先上代码,再根据代码进行解读。
1 using System; 2 using System.Collections.Generic; 3 using System.Linq; 4 using System.Text; 5 using System.Threading.Tasks; 6 7 namespace 堆排序 8 { 9 class Program 10 { 11 public static int[] arr = { 3, 5, 3, 0, 8, 6, 1 }; 12 static void Main(string[] args) 13 { 14 heapSort(arr, arr.Length); 15 foreach (var item in arr) 16 { 17 Console.Write(item + " "); 18 } 19 Console.ReadKey(); 20 } 21 22 public static void heapSort(int []a,int length) 23 { 24 for (int i = length / 2 - 1; i >= 0; --i) // 从最后一个根节点开始,从右往左,从下往上调整 25 { 26 swapSort(arr, i, length); 27 } 28 for(int i=length -1;i>0;--i) 29 { 30 swap(arr, 0, i); // 根元素和尾元素调换 31 swapSort(arr, 0, i-1); // 去掉最后一个元素,重新调整堆结构,调整顺序是从上到下,从左到右 32 } 33 } 34 35 public static void swapSort(int []a,int i,int length) 36 { 37 for(int k=2*i+1;k<length;k=2*k+1) // 从左孩子开始,每次调整结束后,都从该节点下的左孩子开始重新调整下面的结构 @1 38 { 39 if (k+1<length&&arr[k]<arr[k+1]) // 首先找出左孩子和右孩子的最大值 @2 40 { 41 k++; 42 } 43 if (arr[k]>arr[i]) // 如果孩子比根大,则调换位置,且记录被调换孩子的位置,方便调整该孩子下的结构 @3 44 { 45 swap(arr, i, k); 46 i = k; 47 } 48 else 49 { 50 break; 51 } 52 } 53 } 54 55 public static void swap(int []a,int i,int k) 56 { 57 int temp = arr[i]; 58 arr[i] = arr[k]; 59 arr[k] = temp; 60 } 61 } 62 }
其中完成结构调整的部分是
1 public static void heapSort(int []a,int length) 2 { 3 for (int i = length / 2 - 1; i >= 0; --i) // 从最后一个根节点开始,从右往左,从下往上调整 @1 4 { 5 swapSort(arr, i, length); 6 } 7 for(int i=length -1;i>0;--i) // @2 8 { 9 swap(arr, 0, i); // 根元素和尾元素调换 10 swapSort(arr, 0, i-1); // 去掉最后一个元素,重新调整堆结构,调整顺序是从上到下,从左到右 11 } 12 } 13 14 public static void swapSort(int []a,int i,int length) 15 { 16 for(int k=2*i+1;k<length;k=2*k+1) // 从左孩子开始,每次调整结束后,都从该节点下的左孩子开始重新调整下面的结构 @3 17 { 18 if (k+1<length&&arr[k]<arr[k+1]) // 首先找出左孩子和右孩子的最大值 @4 19 { 20 k++; 21 } 22 if (arr[k]>arr[i]) // 如果孩子比根大,则调换位置,且记录被调换孩子的位置,方便调整该孩子下的结构 @5 23 { 24 swap(arr, i, k); 25 i = k; 26 } 27 else 28 { 29 break; 30 } 31 } 32 }
代码解读:
@1:从最后的一个父节点开始调整,如下图:
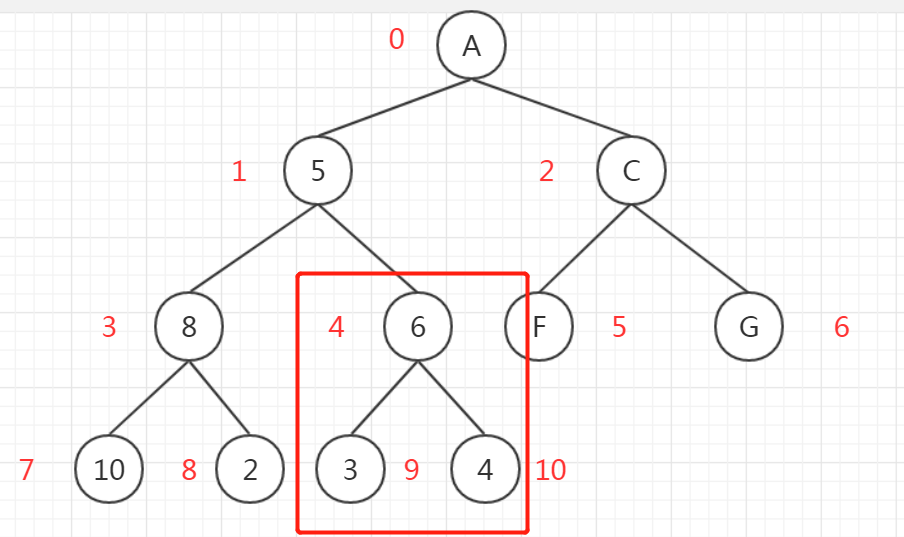
先从4节点开始调整,然后是3结点,直到调整到0结点。
@2:这步是已经建立在建堆完毕之后的步骤,建堆完成之后,首尾元素调换,则最大的元素放到了数集末尾,然后去掉末尾元素的树可能不符合堆的定义,那么就需要重新建堆,因为调整的是根结点,所以调整的步骤就是从上到下,从左到右进行调整而不是之前的方法。
@3,@4,@5:从此步骤开始,就是各个小树的调整,这里做个参数解释:i = 根结点,k = 左孩子,length = 树的长度;从左孩子开始调整,首先比较左孩子和右孩子的大小,如果右孩子比左孩子大,则k右移,然后将右孩子和父结点进行比较,如果孩子结点比父结点大,则交换数值,否则跳出循环即该子树不需要进行调整了赶紧下一个子树吧;看下图:
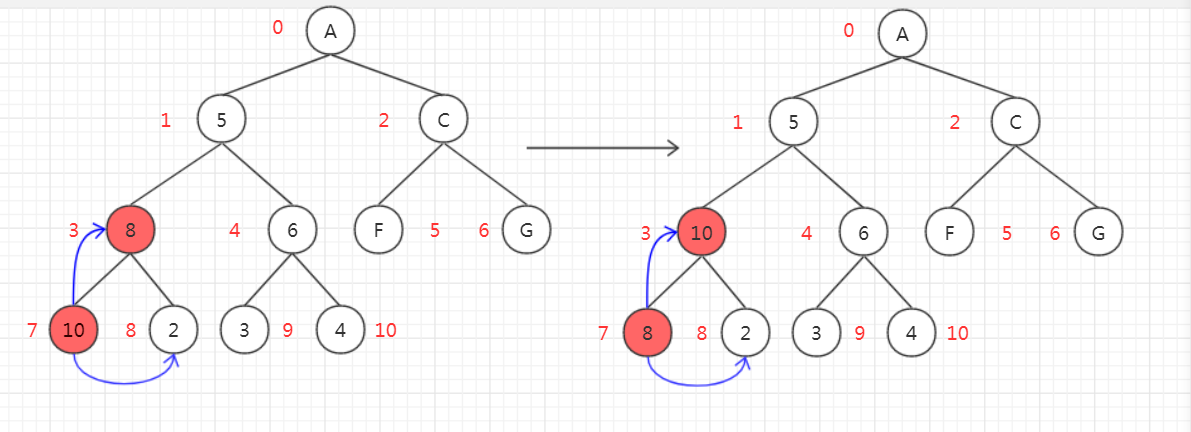
首先比较结点7和结点8的大小,然后比较结点7和结点3的大小,发现孩子比父亲大,所以调整位置;接着继续调整前面的子树(跳过子树2,假设子树2无需调整,直接调整子树1),同样发现结点3大于结点1,那么需要调换,但是因为结点3也是一个根结点,这样调换之后结点3的子树可能会不符合堆定义,看下图:
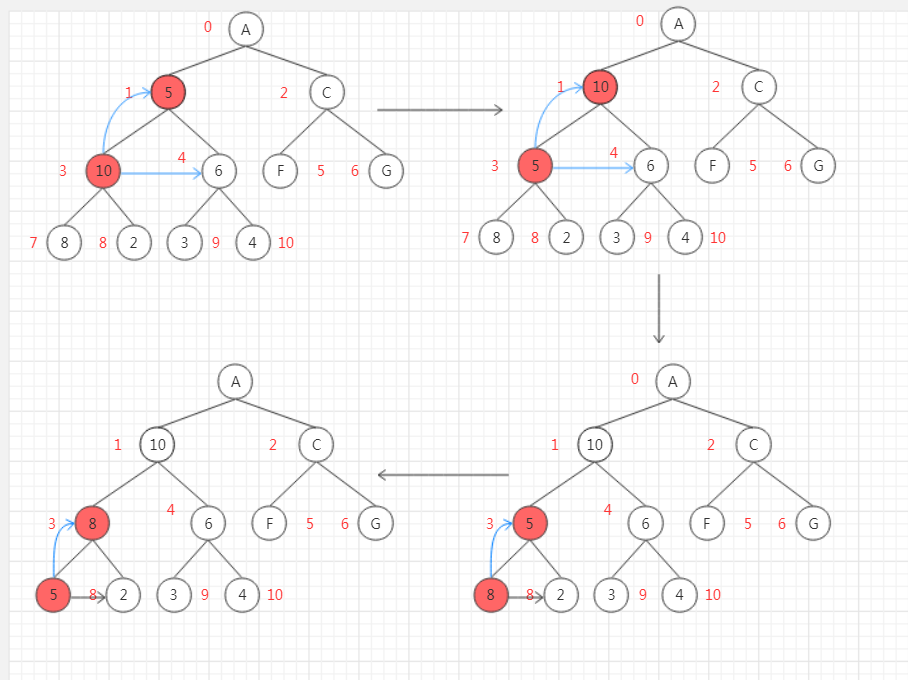
如果调整之后,子树不符合堆定义,那么就继续调整该结点下的子树,直到符合定义为止;所以该for循环的每次循环结束之后都要令 k=2*k+1 ,表示调整了当前的树,就要调整之前被调整结点的子树的左孩子,此时 i = k 就表示 现在需要调整的根结点已经变成了之前调整的孩子结点,比如上图中首先调整了结点3和结点1,在调整之前,i 代表结点1,k代表结点3,调整完成之后,i 代表结点3,k代表结点7,想象一下,如果结点7下面还有许许多多的子树,那么这样赋值 i = k,就可以一直帮我们解决调整的问题。
您可能感兴趣的文章
- 别人用600万换来的收益,我只用了10万,因为选择了它
- 最好的因,可成最坏的果
- 我是一个坏小孩
- 20+的女生,先脱贫还是先脱单?
- 语不惊人死不休(259)心有余闲,不慌张。
- 建立一个优秀的网站的7个用户体验原则
- 我对《哪吒之魔童降世》奇怪的解读角度
- 百度算法调整,关键词大幅波动,怎么办?
未经允许不得转载:杂烩网 » 排序算法——堆排序




