无论是之前学习的MNIST数据集还是Cifar数据集，相比真实环境下的图像识别问题，有两个最大的问题，一是现实生活中的图片分辨率要远高于32*32，而且图像的分辨率也不会是固定的。二是现实生活中的物体类别很多，无论是10种还是100种都远远不够，而且一张图片中不会只出现一个种类的物体。为了更加贴近真实环境下的图像识别问题，由李飞飞教授带头整理的ImageNet很大程度上解决了这个问题。

　　ImageNet是一个基于WordNet的大型图像数据库，在ImageNet中，将近1500万图片被关联到了WorldNet的大约20000个名词同义词集上，目前每一个与ImageNet相关的WordNet同义词集都代表了现实世界中的一个实体，可以被认为是分类问题的一个类别。在ImageNet的图片中，一张图片可能出现多个同义词集所代表的实体。

　　下面主要使用的是ILSVRC2012图像分类数据集，ILSVRC2012图像分类数据集的任务和Cifar数据集是基本一致的，也是识别图像中的主要物体。ILSVRC2012图像分类数据集包含了来自1000个类别的120万张图片，其中每张图片数据且只属于一个类别。因为ILSVRC2012图像分类数据集的图片是直接从互联网上爬取得到的，所以图片的大小从几千字节到几百万字节不等。

卷积神经网络简介

　　为了将只包含全连接层的神经网络和卷积神经网络，循环神经网络区分开，我们将只包含全连接层的神经网络称之为全连接神经网络。下面先学习卷积神经网络与全连接神经网络的差异，并介绍组成一个卷积神经网络的基本网络结构，下图显示了全连接神经网络与卷积神经网络的结构对比图。

　　上图显示的全连接神经网络结构和卷积神经网络的结构直观上差异比较大，但是实际上他们的整体架构是非常相似的。从上图中可以看出，卷积神经网络也是通过一层一层的节点组织起来的。和全连接神经网络一样，卷积神经网络中的每一个节点都是一个神经元。在全连接神经网络中，每相邻两层之间的节点都是有边相连，于是一般会将每层全连接层中的节点组织成一列，这样方便显示连接结构。而对于卷积神经网络，相邻两次之间只有部分节点相连，为了展示每一层神经元的维度，一般会将每一层卷积层的节点组织成一个三维矩阵。

　　除了结构相似，卷积神经网络的输入输出以及训练流程与全连接神经网络也基本一致。以图形分类为例，卷积神经网络的输入层就是图像的原始像素，而输出层中的每一个节点代表了不同类别的可信度。这和全连接神经网络的输入输出是一致的。卷积神经网络和全连接神经网络的唯一区别就在于神经网络中相邻两次的连接方式。

　　下面我们了解一下为什么全连接神经网络无法很好地处理图像数据。

　　使用全连接神经网络处理图像的最大问题在于全连接层的参数太多。对于MNIST数据，每一张图片的大小是28*28*1，其中28*28是图片的大小，*1表示图像是黑白的，只有一个色彩通道。假设第一层隐藏层的节点数为500个，那么一个全连接层的神经网络将有28*28*500+500=392500 个参数。当图片更大时，比如在Cifar-10数据集中，图片的大小为32*32*3，其中32*32表示图片的大小，*3表示图片是通过红绿蓝三个色彩通道（channel）表示的。这样输入层就是3072个节点，如果第一次全连接层仍然是500个节点，那么这一层全连接神经网络将有32*32*3*500+500=150万个参数（大约）。参数增多除了导致计算速度减慢，还很容易导致过拟合问题。所以需要一个更合理的神经网络结构来有效的减少神经网络中参数个数。而卷积神经网络就可以达到这个目的。

　　下面给出了一个更加具体的神经网络架构图：

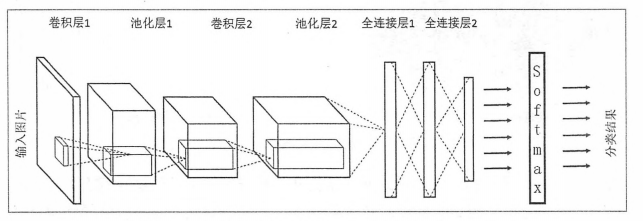
　　在卷积神经网络的前几层中，每一层的节点都被组织成一个三维矩阵。比如处理Cifar-10数据集中的图片时，可以将输入层组织成一个32*32*3的三维矩阵。上图的虚线部分展示了卷积神经网络的一个连接示意图，从图中可以看出卷积神经网络中前几层中每一个节点只和上一层中部分的节点相连。

　　下面给出一个卷积神经网络主要由以下五种结构组成：

　　1，输入层。输入层是整个神经网络的输入，在处理图像的卷积神经网络中，它一般代表了一张图片的像素矩阵。比如在上图中最左侧的三维矩阵就是可以代表一张图片。其中三维矩阵的长和宽代表了图像的大小，而三维矩阵的深度代表了图像的色彩通道（channel）。比如黑白图片的深度为1，而在RGB色彩模式下，图像的深度为3。从输入层开始，卷积神经网络通过不同的神经网络结构将上一层的三维矩阵转化为下一层的三维矩阵，直到最后的全连接层。

　　2，卷积层。从名字就可以看出，卷积层是一个卷积神经网络中最为重要的部分，和传统全连接层不同，卷积层是一个卷积神经网络中最为重要的部分，和传统全连接层不同，卷积层中每一个节点的输入只是上一层神经网络的一小块，这个小块常用的大小有3*3或者5*5.卷积层试图将神经网络中的每一小块进行更加深入的分析从而得到抽象程度更高的特征。一般来说，通过卷积层处理过的节点矩阵会变得更深，所以上图可以看到经过卷积层之后的节点矩阵的深度会增加。

　　3，池化层（Pooling）。池化层神经网络不会改变三维矩阵的深度，但是它可以缩小矩阵的大小。池化操作可以认为是将一张分辨率较高的图片转化为分辨率较低的图片。通过池化层，可以进一步缩小最后全连接层中节点的个数，从而达到减少整个神经网络中参数的目的。

　　4，全连接层，经过多轮卷积层和池化层的处理之后，在卷积神经网络的最后一般会是由1到2个全连接层来给出最后的分类结果。经过几轮卷积层和池化层的处理之后，可以认为图像中的信息以及抽象成了信息含量更高的特征。我们可以将卷积层和池化层看出自动图像特征提取的过程。在特征提取完成之后，让然需要使用全连接层来完成分类任务。

　　5，Softmax层，Softmax层主要用于分类问题，通过Softmax层，可以得到当前样例属于不同种类的概率分布情况。

卷积神经网络常用结构——卷积层

　　本小节将详细介绍卷积层的结构以及前向传播的算法，下图显示了卷积层神经网络结构中最为重要的部分，这个部分被称之为过滤器（filter）或者内核（kernel）。因为TensorFlow文档中将这个结构称为过滤器（filter），所以我们本文就称为过滤器。如图所示，过滤器可以将当前层神经网络的一个子节点矩阵转化为下一层神经网络上的一个单位节点矩阵。单位节点矩阵指的是一个长和宽都是1，但是深度不限的节点矩阵。

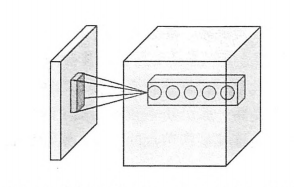
　　在一个卷积层中，过滤器所处理的节点矩阵的长和宽都是由人工指定的，这个节点矩阵的尺寸也被称之为过滤器的尺寸。常用的过滤器尺寸有3*3或者5*5。因为过滤器处理的矩阵深度和当前层神经网络节点矩阵的深度是一致的，所以虽然节点矩阵是三维的，但过滤器的尺寸只需要指定两个维度。过滤器中另外一个需要人工指定的设置是处理得到的单位节点矩阵的深度，这个设置称为过滤器的深度。注意过滤器的尺寸指的是一个过滤器输入节点矩阵的大小。而深度指的就是输出单位节点矩阵的深度。如图所示，左侧小矩阵的尺寸为过滤器的尺寸，而右侧单位矩阵的深度为过滤器的深度。

　　如图所示，过滤器的前向传播过程就是通过左侧小矩阵中的节点计算出右侧单位矩阵中的节点的过程。为了直观的解释过滤器的前向传播过程。下面给出一个样例，在这个样例中将展示如何通过过滤器将一个2*2*3的节点矩阵转化为一个1*1*5的单位节点矩阵，一个过滤器的前向传播过程和全连接层相似，它总共需要 2*2*3*5+5=65个参数，其中最后的+5为偏置项参数的个数，假设使用 来表示对于输出单位节点矩阵中的第 i 个节点，过滤器输入节点 （x, y ,z）的权重，使用 bⁱ   表示第 i 个输出节点对应的偏置项参数，那么单位矩阵中的第 i 个节点的取值为 g(i) 为：

　　其中，为过滤器中节点（x, y ,z）的取值，f 为激活函数，下图展示了在给定 a , w⁰ 和 b⁰ 的情况下，使用ReLU作为激活函数时 g(0) 的计算过程。在图中给出了 a 和 w⁰ 的取值，这里通过三个二维矩阵来表示一个三维矩阵的取值，其中每一个二维矩阵表示三维矩阵中在某一个深度上的取值。图中 • 符号表示点积，也就是矩阵中对应元素乘积的和，下图右侧显示了 g(0) 的计算过程，如果给出 w¹到 w⁴ 和 b¹ 到 b⁴ ，那么也可以类似地计算出 g(1)到 g(4) 的取值。如果将 a 和 wⁱ 组织成两个向量，那么一个过滤器的计算过程完全可以通向量乘积完成。

　　上面的样例已经学习了在卷积层中计算一个过滤器的前向传播过程。卷积层结构的前向传播就是通过将一个过滤器从神经网络当前层的左上角移动到右下角，并且在移动中计算每一个对应的单位矩阵得到的。下图展示了卷积层结构前向传播的过程。为了更好的可视化过滤器的移动过程，图中使用的节点矩阵深度都是1。在图中展示了在3*3矩阵上使用2*2过滤器的卷积前向传播过程，在这个过程中，首先将这个过滤器用于左上角子矩阵，然后移动到左下角矩阵，再到右上角矩阵，最后到右下角矩阵。过滤器每移动一次，可以计算得到一个值（当深度为 k 时会计算出 k 个值）。将这些数值拼成一个新的矩阵，就完成了卷积层前向传播的过程。图中右侧显示了过滤器在移动过程中计算得到的结果与新矩阵中节点的对应关系。

　　当过滤器的大小不为1*1时，卷积层前向传播得到的矩阵的尺寸要小于当前层矩阵的尺寸。如上图所示，当前层矩阵的大小为3*3，而通过卷积层前向传播算法之后，得到的矩阵大小为2*2。为了避免尺寸的变化，可以在当前层矩阵的边界上加入全0填充（zero-padding）。这样可以使得卷积层前向传播结果矩阵的大小和当前层矩阵保持一致。

　　下图显示了使用全0填充后卷积层前向传播过程示意图，从图中可以看出，加入一层全0填充后，得到的结构矩阵大小就为3*3了。

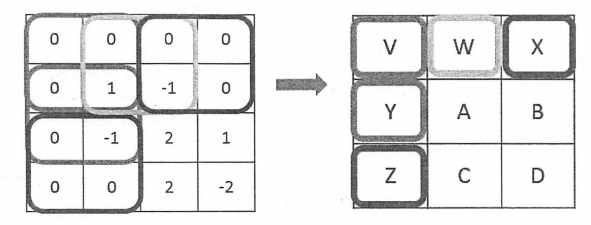
　　除了使用全0填充，还可以通过设置过滤器移动的步长来调整结果矩阵的大小。在上图中，过滤器每次都只移动一格，下图显示了当移动步长为2且使用全0填充时，卷积层前向传播的过程。

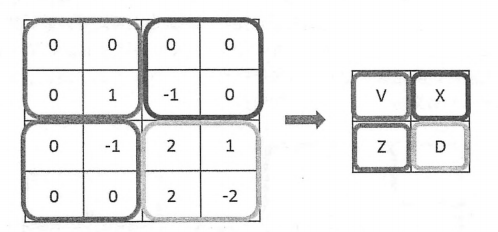
　　从上图可以看出，当长和宽的步长均为2时，过滤器每隔2步计算一次结果，所以得到的结果矩阵的长和宽也就只有原来的一半。下面的公式给出了在同时使用全0填充时结果矩阵的大小：

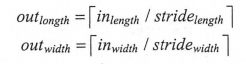
　　其中out_height 表示输出层矩阵的长度，它等于输入层矩阵长度除以长度方向上的步长的向上取整值。类似的，out_height 表示输出层矩阵的宽度，它等于输入层矩阵宽度除以宽度方向上的步长的向上取整值。如果不使用全0填充，下面的公式给出了结果矩阵的大小：

　　在上面，只有移动过滤器的方式，没有涉及到过滤器中的参数如何设定，所以在这些图片中结果矩阵中并没有填上具体的值。在卷积神经网络中，每一个卷积层中使用的过滤器中的参数都是一样的。这是卷积神经网络一个非常重要的性质。从直观上立即额，共享过滤器的参数可以使得图像上的内容不受位置的影响。以MNIST手写体数字识别为例，无论数字“1”出现在左上角还是右下角，图片的种类都是不变的。因为在左上角和右下角使用的过滤器参数相同，所以通过卷积层之后无论数字在图像上的那个位置，得到的结果都一样。

　　共享每一个卷积层中过滤器中的参数可以巨幅减少神经网络上的参数。以Cifar-10问题为例，输入层矩阵的维度是32*32*3.假设第一层卷积使用尺寸为5*5，深度为16的过滤器，那么这个卷积层的参数个数为5*5*3*16+16=1216 个。上面提到过，使用500个隐藏层节点的全连接层将有1.5百万个参数。相比之下，卷积层的参数个数要远远小于全连接层。而且卷积层的参数个数和图片的大小无关，它之和过滤器的尺寸，深度以及前档层节点矩阵的深度有关。这使得卷积神经网络可以很好的扩展到更大的图像数据上。

　　结合过滤器的使用方法和参数共享机制，下图给出了使用全0填充，步长为2的卷积层前向传播的计算流程。

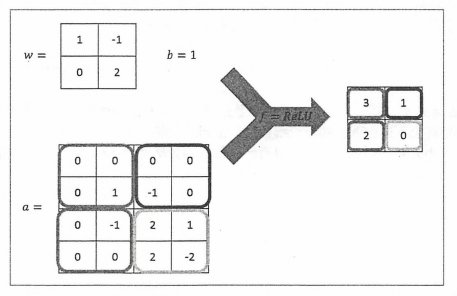
　　下图给出了过滤器上权重以及偏置项的取值，通过图中所示的计算方法，可以得到每一个格子的具体取值。下面公式给出了左上角格子取值的计算方法，其他格子可以依次类推。

　　TensorFlow对卷积神经网络提供了非常好的支持，下面程序实现了一个卷积层的前向传播过程，从下面代码可以看出，通过TensorFlow实现卷积层是非常方便的。

#_*_coding:utf-8_*_  import tensorflow as tf    # 通过 tf.get_variable 的方式创建过滤器的权重变量和偏置项变量  # 卷积层的参数个数只和过滤器的尺寸，深度以及当前层节点矩阵的深度有关  # 所以这里声明的参数变量是一个四位矩阵，前面两个维度代表了过滤器的尺寸  # 第三个维度表示当前层的深度，第四个维度表示过滤器的深度  filter_weight = tf.get_variable(      'weights', [5, 5, 3, 16],      initializer=tf.truncated_normal_initializer(stddev=0.1)  )  # 和卷积层的权重类似，当前层矩阵上不同位置的偏置项也是共享的，所以总共有下一层深度个不同的偏置项  # 下面样例中16为过滤器的深度，也是神经网络中下一层节点矩阵的深度  biases = tf.get_variable(      'biases', [16],      initializer=tf.truncated_normal_initializer(0.1)  )    # tf.nn.conv2d 提供了一个非常方便的函数来实现卷积层前向传播的算法  # 这个函数的第一个输入为当前层的节点矩阵。注意这个矩阵是一个思维矩阵  # 后面三个维度对应一个节点矩阵，第一个对应一个输入batch  # 比如在输入层，input[0, :, :, :]表示第一张图片 input[1. :, :, :]表示第二章图片  # tf.nn.conv2d 第二个参数提供了卷积层的权重，第三个参数为不同维度上的步长  # 虽然第三个参数提供的是一个长度为4的数组，但是第一维和最后一维的数字要求一定是1  # 这是因为卷积层的步长只对矩阵的长和宽有效，最后一个参数是填充（padding）的方法  # TensorFlow中提供SAME 或者VALID 两种选择，SAME 表示填充全0 VALID表示不添加  conv = tf.nn.conv2d(      input, filter_weight, strides=[1, 1, 1, 1], padding='SAME'  )    # tf.nn.bias_add 提供了一个方便的函数给每一个节点加上偏置项  # 注意这里不能直接使用加法，因为矩阵上不同位置上的节点都需要加上同样的偏置项  # 虽然下一层神经网络的大小为2*2，但是偏置项只有一个数（因为深度为1）  # 而2*2矩阵中的每一个值都需要加上这个偏置项  bias = tf.nn.bias_add(conv, biases)  # 将计算结果通过ReLU激活函数完成去线性化  actived_conv = tf.nn.relu(bias)  

卷积神经网络常用结构——池化层

 　　池化层可以非常有效的缩小矩阵的尺寸，从而减少最后全连接层的参数，使用池化层既可以加快计算速度也有效防止过拟合问题的作用。

　　池化层前向传播的过程也是通过移动一个类似过滤器的结构完成的，不过池化层过滤器的计算不是节点的加权和，而是采用更加简单的最大值或者平均值计算。使用最大值操作的池化层被称为最大池化层（max  pooling），这是被使用得最多的池化层结构。使用平均值操作的池化层被称之为平均池化层（average pooling）。其他池化层在实践中使用比较少。

　　与卷积层的过滤器类似，池化层的过滤器也需要人工设定过滤器的尺寸，是否使用全0填充以及过滤器移动的步长等设置，而且这些设置的意义也是一样的。卷积层和池化层中过滤器移动的方式是相似的，唯一的区别在于卷积层使用的过滤器是横跨整个深度的，而池化层使用的过滤器只影响一个深度上的节点。所以池化层的过滤器除了在长和宽两个维度移动之外，它还需要在深度这个维度移动。下图展示了一个最大池化层前向传播计算过程。

　　在上图中，不同颜色或者不同线段（虚线或者实线）代表了不同的池化层过滤器。从图中可以看出，池化层的过滤器除了在长和宽的维度上移动，它还需要在深度的维度上移动。下面TensorFlow程序实现了最大池化层的前向传播算法。

# tf.nn.max_pool 实现了最大池化层的前向传播过程，他的参数和 tf.nn.conv2d函数类似  #ksize 提供了过滤器的尺寸，strides提供了步长信息，padding提供了是否使用全0填充  pool = tf.nn.max_pool(actived_conv, ksize=[1, 3, 3, 1],                        strides=[1, 2, 2, 1], padding='SAME')  

　　对比池化层和卷积层前向传播在TensorFlow中的实现，可以发现函数的参数形式是相似的。在tf.nn.max_pool 函数中，首先需要传入当前层的节点矩阵，这个矩阵是一个四维矩阵，格式和 tf.nn.conv2d 函数的第一个参数一致。第二个参数为过滤器的尺寸，虽然给出的是一个长度为4的一维数组，但是这个数组的第一个和最后一个数必须为1。这意味着池化层的过滤器是不可以跨不同输入样例或者节点矩阵深度的。在实际应用中使用的最多的池化层过滤器尺寸为 [1, 2, 2, 1] 或者 [1, 3, 3, 1]。

　　tf.nn.max_pool 函数的第三个参数为步长，它和 tf.nn.conv2d 函数中步长的意义是一样的，而且第一维和最后一维也只能为1。这意味着在TensorFlow中，池化层不能减少节点矩阵的深度或者输入样例的个数。tf.nn.max_pool函数的最后一个参数指定了是否使用全0填充。这个参数也只能有两种取值——VALID或者SAME。其中VALID表示不使用全0填充，SAME表示使用全0填充。TensorFlow还提供了 tf.nn.avg_pool来实现平均池化层。其调用格式和之前介绍的一样。

经典卷积网络模型——LeNet-5模型

　　下面学习LeNet模型，并给出一个完整的TensorFlow程序来实现LeNet-5模型，通过这个模型，将给出卷积神经网络结构设计的一个通用模式，然后再学习设计卷积神经网络结构的另外一种思路——Inception模型。

LeNet网络背景

　　LeNet诞生于1994年，由深度学习三巨头之一的Yan LeCun提出，他也被称为卷积神经网络之父。LeNet主要用来进行手写字符的识别与分类，准确率达到了98%，并在美国的银行中投入了使用，被用于读取北美约10%的支票。LeNet奠定了现代卷积神经网络的基础。它是第一个成功应用于数字识别问题的卷积神经网络。在MNIST数据集上，LeNet-5模型可以达到大约99.2%的正确率。LeNet-5模型总共有7层，下图展示了LeNet-5模型架构：

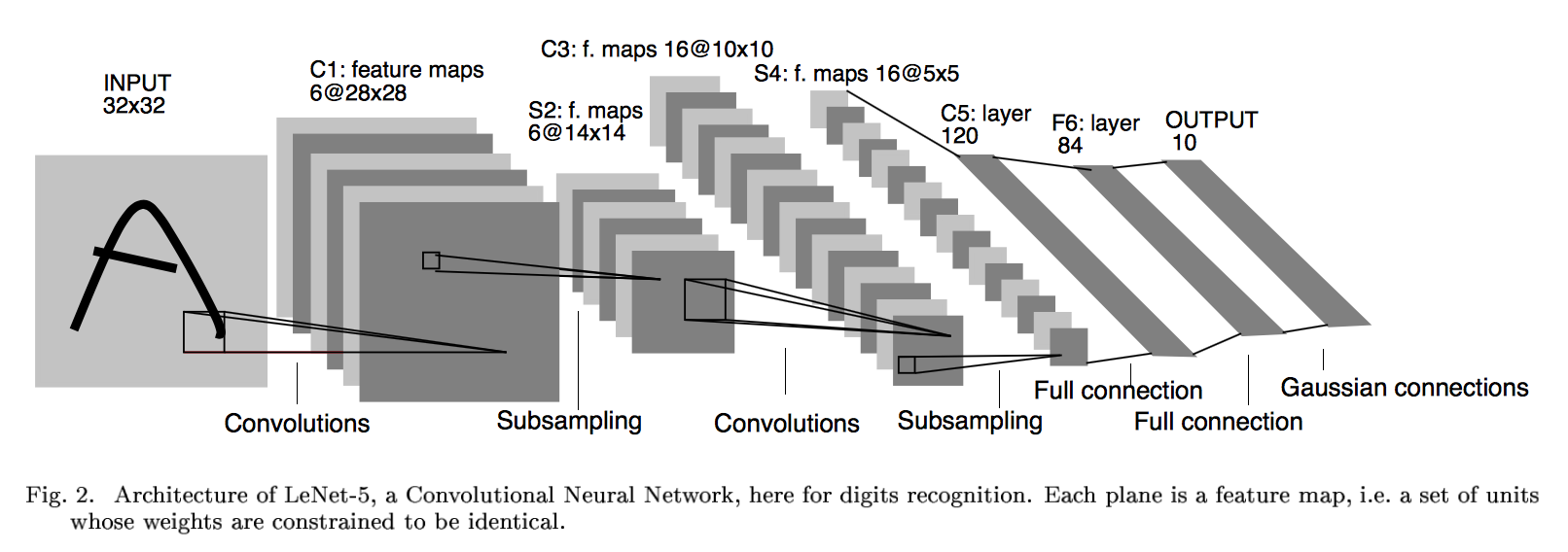
LeNet网络结构

　　第一层：卷积层

 　　这一层的输入就是原始的图像像素，LeNet-5 模型接受的输入层大小为32*32*1。第一层卷积层过滤器的尺寸为5*5，深度为6，不使用全0填充，步长为1。因为没有使用全0填充，所以这一层的输出的尺寸为32-5+1=28，深度为6。这一个卷积层总共有5*5*1*6+6=156 个参数，其中6个未偏置项参数，因为下一层的节点矩阵有28*28*6=4704 个节点，每个节点和 5*5=25 个当前层节点相连，所以本层卷积层共有 （5*5*1）*6*（28*28）=122304 个连接。

　　第二层：池化层

　　这一层的输入为第一层的输出，是一个28*28*6 的节点矩阵。本层采用的过滤器大小为2*2，长和宽的步长均为2，所以本层的输出矩阵大小为14*14*6。

　　第三层：卷积层

　　本层的输入矩阵大小为14*14*6，使用的过滤器大小为5*5，深度为16。本层不使用全0填充，步长为1。本层的输出矩阵大小为10*10*16 。按照标准的卷积层，本层应该有5*5*6*16+16=2416 个参数，10*10*16*（25+1）=41600 个连接。

　　第四层：池化层

　　本层的输入矩阵大小为10*10*16，采用的过滤器大小为2*2，步长为2，本层的输出矩阵大小为5*5*16。

　　第五层：全连接层

　　本层的输入矩阵大小为5*5*16，在LeNet-5 模型的论文中将这一层称为卷积层，但是因为过滤器的大小就是5*5 ， 所以和全连接层没有区别，在之后的TensorFlow程序实现中也会将这一层看成全连接层。如果将5*5*16 矩阵中的节点拉成一个向量，那么这一层和之前学习的全连接层就一样的了。本层的输出节点个数为120个，总共有5*5*16*120+120=48120 个参数。

　　第六层：全连接层

　　本层的输入节点个数为120个，输出节点个数为84个，总共参数为120*84+84=10164 个。

　　第七层：全连接层

　　本层的输入节点个数为84个，输出节点个数为10个，总共参数为84*10+10=850个。

 　　上面介绍了LeNet-5模型每一层结构和设置，下面给出TensorFlow的程序来实现一个类似LeNet-5 模型的卷积神经网络来解决MNIST数字识别问题。通过TensorFlow训练卷积神经网络的过程和之前学习的是一样的。损失函数和反向传播过程的实现均可以复用其代码。唯一的区别就是卷积神经网络的输入层是一个三维矩阵，所以需要调整一下输入数据的格式。

下面看一下代码。

　　mnist_train.py

#_*_coding:utf-8_*_  import os  import tensorflow as tf  from tensorflow.examples.tutorials.mnist import input_data    # 加载 bookmnist_inference.py 中定义的常量和前向传播的函数  import bookmnist_inferencecnn as bookmnist_inference  import numpy as np    # 配置神经网络的参数  BATCH_SIZE = 100  # 基础的学习率，使用指数衰减设置学习率  LEARNING_RATE_BASE = 0.01  # 0.8  # 学习率的初始衰减率  LEARNING_RATE_DECAY = 0.99  REGULARAZTION_RATE = 0.0001  # 训练轮数  TRAINING_STEPS = 30000  # 滑动平均衰减值  MOVING_AVERAGE_DECAY = 0.99  # 模型保存的路径和文件名  MODEL_SAVE_PATH = 'model_cnn1/'  if not os.path.exists(MODEL_SAVE_PATH):      os.mkdir(MODEL_SAVE_PATH)  MODEL_NAME = 'model.ckpt'        def train(mnist):      # 调整输入数据placeholder的格式，输入为一个四维矩阵      x = tf.placeholder(tf.float32, [          BATCH_SIZE,  # 第一维表示一个batch中样例的个数          bookmnist_inference.IMAGE_SIZE,  # 第二维和第三维表示图片的尺寸          bookmnist_inference.IMAGE_SIZE,          bookmnist_inference.NUM_CHANNELS  # 第四维表示图片的深度，对于RGB格式的图片，深度为5      ], name='x-input')        y_ = tf.placeholder(          tf.float32, [None, bookmnist_inference.OUTPUT_NODE], name='y-input'      )        regularizer = tf.contrib.layers.l2_regularizer(REGULARAZTION_RATE)      # 直接使用bookmnost_inference.py中定义的前向传播过程      y = bookmnist_inference.inference(x, False,  regularizer)      global_step = tf.Variable(0, trainable=False)        # 定义损失函数，学习率，滑动平均操作以及训练过程      variable_averages = tf.train.ExponentialMovingAverage(          MOVING_AVERAGE_DECAY, global_step      )      variable_averages_op = variable_averages.apply(          tf.trainable_variables()      )      cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(          logits=y, labels=tf.argmax(y_, 1)      )      cross_entropy_mean = tf.reduce_mean(cross_entropy)      loss = cross_entropy_mean + tf.add_n(tf.get_collection('losses'))      learning_rate = tf.train.exponential_decay(          LEARNING_RATE_BASE,          global_step,          mnist.train.num_examples / BATCH_SIZE,          LEARNING_RATE_DECAY      )      train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(          loss, global_step=global_step      )      with tf.control_dependencies([train_step, variable_averages_op]):          train_op = tf.no_op(name='train')        # 初始化TensorFlow持久化类      saver = tf.train.Saver()      with tf.Session() as sess:          tf.global_variables_initializer().run()            # 在训练过程中不再测试模型在验证数据上的表现          # 验证和测试的过程都将会有一个独立的程序完成          for i in range(TRAINING_STEPS):              xs, ys = mnist.train.next_batch(BATCH_SIZE)              # 类似的将输入的训练数据格式调整为一个四维矩阵，并将这个调整后的数据传入 sess.run 过程              reshaped_xs = np.reshape(xs, (BATCH_SIZE,                                            bookmnist_inference.IMAGE_SIZE,                                            bookmnist_inference.IMAGE_SIZE,                                            bookmnist_inference.NUM_CHANNELS                                            ))                _, loss_value, step = sess.run([train_op, loss, global_step],                                             feed_dict={x: reshaped_xs, y_: ys})              # 每1000轮保存一次模型              if i % 1000 == 0:                  # 输出当前的训练情况，这里只输出了模型在当前训练batch上的损失函数大小                  # 通过损失函数的大小可以大概了解训练的情况，在验证集上正确率信息会有一个单独的程序来生成                  print("Afer %d training step(s), loss on training batch is %g"%(step, loss_value))                    # 保存当前模型，注意这里给出的global_step参数，这样可以让每个被保存模型的文件名末尾加上训练点额轮数                  saver.save(                      sess, os.path.join(MODEL_SAVE_PATH, MODEL_NAME),                      global_step=global_step                  )    def main(argv=None):      mnist = input_data.read_data_sets('data', one_hot=True)      train(mnist)      if __name__ == '__main__':      main()  

　　得到的输出如下：

Extracting datatrain-images-idx3-ubyte.gz  Extracting datatrain-labels-idx1-ubyte.gz  Extracting datat10k-images-idx3-ubyte.gz  Extracting datat10k-labels-idx1-ubyte.gz  Afer 1 training step(s), loss on training batch is 4.79052  Afer 1001 training step(s), loss on training batch is 0.710321  Afer 2001 training step(s), loss on training batch is 0.697147  Afer 3001 training step(s), loss on training batch is 0.701041  Afer 4001 training step(s), loss on training batch is 0.633242  Afer 5001 training step(s), loss on training batch is 0.638359  Afer 6001 training step(s), loss on training batch is 0.63794  Afer 7001 training step(s), loss on training batch is 0.663004  ... ...  Afer 29001 training step(s), loss on training batch is 0.631867  

　mnist_inference.py的代码：

#_*_coding:utf-8_*_  import tensorflow as tf    # 定义神经网络结构相关参数  INPUT_NODE = 784         # 28*28=784  OUTPUT_NODE = 10    IMAGE_SIZE = 28  NUM_CHANNELS = 1  NUM_LABELS = 10    # 第一层卷积层的尺寸和深度  CONV1_DEEP = 32  CONV1_SIZE = 5    # 第二层卷积层的尺寸和深度  CONV2_DEEP = 64  CONV2_SIZE = 5    # 全连接层的节点个数  FC_SIZE = 512      # 定义神经网络的前向传播过程 这里添加了一个新的参数 train 用于区分训练过程和测试过程  # 在这个程序中将用到 droput方法，dropout可以进一步提升模型可靠性并防止过拟合  # droput过程只在训练时使用  def inference(input_tensor, train, regularizer):      # 声明第一层卷积层的变量并实现前向传播过程      # 通过使用不同的命名空间来隔离不同层的变量，这可以让每一层中的变量命名      # 只需要考虑在当前层的作用，而不需要担心重名的问题      # 和标准的LeNet-5模型不大一样，这里定义的卷积层输入为28*28*1的原始MNIST图片像素      # 因为卷积层中使用了全0填充，所以输出为28*28*32的矩阵      with tf.variable_scope('layer1-conv1'):          conv1_weights = tf.get_variable(              'weight', [CONV1_SIZE, CONV1_SIZE, NUM_CHANNELS, CONV1_DEEP],              initializer=tf.truncated_normal_initializer(stddev=0.1)          )          conv1_biases = tf.get_variable(              'bias', [CONV1_DEEP],              initializer=tf.constant_initializer(0.0)          )          # 使用边长为5，深度为32的过滤器，过滤器移动的步长为1，且使用全0填充          conv1 = tf.nn.conv2d(              input_tensor, conv1_weights, strides=[1, 1, 1, 1], padding='SAME'          )          relu1 = tf.nn.relu(tf.nn.bias_add(conv1, conv1_biases))        # 实现第二层池化层的前向传播过程，这里选用最大池化层，池化层过滤器的边长为2      # 使用全0填充且移动的步长为2，这一层的输入时上一层的输出，也就是28*28*32的矩阵      # 输出为14*14*32的矩阵      with tf.name_scope('layer2-pool1'):          pool1 = tf.nn.max_pool(              relu1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME'          )        # 声明第三层卷积层的变量并实现前向传播过程，这一层的输入为14*14*32 的矩阵      # 输出为14*14*64      with tf.variable_scope('layer3-conv2'):          conv2_weights = tf.get_variable(              'weight', [CONV2_SIZE, CONV2_SIZE, CONV1_DEEP, CONV2_DEEP],              initializer=tf.truncated_normal_initializer(stddev=0.1)          )          conv2_biases = tf.get_variable(              'bias', [CONV2_DEEP],              initializer=tf.constant_initializer(0.0)          )            # 使用边长为5， 深度为64的过滤器，过滤器移动的步长为1，且使用全0填充          conv2 = tf.nn.conv2d(              pool1, conv2_weights, strides=[1, 1, 1, 1], padding='SAME'          )          relu2 = tf.nn.relu(tf.nn.bias_add(conv2, conv2_biases))        # 实现第四层池化层的前向传播过程，这一层和第二层的结构是一样的，      # 这一层的输入为14*14*64 的矩阵，输出为7*7*64 的矩阵      with tf.name_scope('layer4-pool2'):          pool2 = tf.nn.max_pool(              relu2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME'          )        # 将第四层池化层的输出转化为第五层全连接层的输入格式，第四层的输出为7*7*64 的矩阵      # 然而第五层全连接层需要的输入格式为向量，所以在这里需要将这个7*7*64 的矩阵拉直成一个向量      # pool2.get_shape 函数可以得到第四层输出矩阵的维度而不需要手工计算      # 注意因为每一层神经网络的输出输入都是一个 batch的矩阵，      # 所以这里得到的维度也包含了一个batch中的数据的个数      pool_shape = pool2.get_shape().as_list()      # 计算将矩阵拉直成项链之后的长度，这个长度就是矩阵长宽及深度的乘积      # 注意这里 pool_shape[0] 为一个batch中数据的个数      nodes = pool_shape[1] * pool_shape[2] * pool_shape[3]        # 通过 tf.reshape 函数将第四层的输出变成一个 batch 项链      reshaped = tf.reshape(pool2, [pool_shape[0], nodes])        # 声明第五层全连接层的变量并实现前向传播过程，这一层的输入时拉直之后的一组向量      # 向量长度为3136，输出是一组长度为512 的向量      # 这里引入了dropout的概念，dropout在训练时会随机将部分节点的输出改为0      # dropout 可以避免过拟合问题，从而使得模型在测试数据上的效果更好      # dropout 一般只在全连接层而不是卷积层或者池化层使用      with tf.variable_scope('layer5-fc1'):          fc1_weights = tf.get_variable(              'weight', [nodes, FC_SIZE],              initializer=tf.truncated_normal_initializer(stddev=0.1)          )          # 只有全连接层的权重需要加入正则化          if regularizer != None:              tf.add_to_collection('losses', regularizer(fc1_weights))          fc1_biases = tf.get_variable(              'bias', [FC_SIZE], initializer=tf.constant_initializer(0.1)          )          fc1 = tf.nn.relu(tf.matmul(reshaped, fc1_weights) + fc1_biases)          if train:              fc1 = tf.nn.dropout(fc1, 0.5)        # 声明第六层全连接层的变量并实现前向传播过程，这一层的输入为一组长度为512的向量      # 输出为一组长度为10的向量，这一层的输出通过softmax之后就得到了最后的分类结果      with tf.variable_scope('layer6-fc2'):          fc2_weights = tf.get_variable(              'weight', [FC_SIZE, NUM_LABELS],              initializer=tf.truncated_normal_initializer(stddev=0.1)          )          if regularizer != None:              tf.add_to_collection('losses', regularizer(fc2_weights))          fc2_biases = tf.get_variable(              'bias', [NUM_LABELS],              initializer=tf.constant_initializer(0.1)          )          logit = tf.matmul(fc1, fc2_weights) + fc2_biases        # 返回第六层的输出      return logit  

　　mnist_eval.py

#_*_coding:utf-8_*_  import time  import tensorflow as tf  from tensorflow.examples.tutorials.mnist import input_data    # 加载 mnist_inference.py 和 mnist_train.py中定义的常量和函数  import bookmnist_inferencecnn as bookmnist_inference  import bookmnist_traincnn as bookmnist_train  import numpy as np    # 每10秒加载一次最新的模型，并在测试数据上测试最新模型的正确率  EVAL_INTERVAL_SECS = 10    def evalute(mnist):      with tf.Graph().as_default() as g:          # 定义输入输出格式，调整输入数据的格式，输入为一个四维矩阵          x = tf.placeholder(              tf.float32, [                  bookmnist_train.BATCH_SIZE,                      # 第一维表示一个batch中样例的个数                  bookmnist_inference.IMAGE_SIZE,  # 第二维和第三维表示图片的尺寸                  bookmnist_inference.IMAGE_SIZE,                  bookmnist_inference.NUM_CHANNELS  # 第四维表示图片的深度，对于RGB格式的图片，深度为5              ], name='x-input'          )          y_ = tf.placeholder(              tf.float32, [None, bookmnist_inference.OUTPUT_NODE], name='y-input'          )            xs, ys = mnist.test.next_batch(bookmnist_train.BATCH_SIZE)          reshape_xs = np.reshape(xs, (bookmnist_train.BATCH_SIZE,                                       bookmnist_inference.IMAGE_SIZE,                                       bookmnist_inference.IMAGE_SIZE,                                       bookmnist_inference.NUM_CHANNELS                                       ))          validate_feed = {x: reshape_xs, y_: ys}            # 直接通过调用封装好的函数来计算前向传播的额结果          #因为测试时不关注正则化损失的值，所以这里用于计算正则化损失函数被设置为None          y = bookmnist_inference.inference(x, False, None)            # 使用前向传播的结果计算正确率，如果需要对未知的样本进行分类，          # 那么使用 tf.argmax(y, 1)就可以得到输入样例的预测类别了          # 判断两个张量的每一维是否相等，如果相等就返回True，否则返回False          correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))          accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))            # 通过变量重命名的方式来加载模型，这样在前向传播的过程中就不需要调用求滑动平均的函数获取平均值          # 这样就可以完全共享之前mnist_inference.py中定义的前向传播过程          variable_averages = tf.train.ExponentialMovingAverage(              bookmnist_train.MOVING_AVERAGE_DECAY          )          variables_to_restore = variable_averages.variables_to_restore()          saver = tf.train.Saver(variables_to_restore)            # 每隔EVAL_INTERVAL_SECS 秒调用一次计算正确率的过程以检测训练过程中正确率的变化          while True:              with tf.Session() as sess:                  # tf.train.get_checkpoint_state函数会通过checkpoint文件                  # 自动找到目录中最新模型的文件名                  ckpt = tf.train.get_checkpoint_state(                      bookmnist_train.MODEL_SAVE_PATH                  )                  if ckpt and ckpt.model_checkpoint_path:                      # 加载模型                      saver.restore(sess, ckpt.model_checkpoint_path)                      # 通过文件名得到模型保存时迭代的轮数                      global_step = ckpt.model_checkpoint_path.split('/')[-1].split('-')[-1]                      accuracy_score = sess.run(accuracy, feed_dict=validate_feed)                      print("After %s training step(s) , validation accuracy ='%g"%(global_step, accuracy_score))                  else:                      print("No checkpoint file found")                      return                  time.sleep(EVAL_INTERVAL_SECS)    def main(argv=None):      mnist = input_data.read_data_sets('data', one_hot=True)      evalute(mnist)      if __name__ == '__main__':      main()  

　　运行测试代码，得到的结果如下：

Extracting datatrain-images-idx3-ubyte.gz  Extracting datatrain-labels-idx1-ubyte.gz  Extracting datat10k-images-idx3-ubyte.gz  Extracting datat10k-labels-idx1-ubyte.gz  After 29001 training step(s) , validation accuracy ='1  After 29001 training step(s) , validation accuracy ='1  After 29001 training step(s) , validation accuracy ='1  

　　在MNIST测试数据集上，上面的卷积神经网络可以达到大约   100% 的正确率，。相比较全连接层的98.4%的正确率，卷积神经网络可以巨幅提高神经网络在MNIST数据集上的正确率。

LeNet-5 总结

• LeNet-5是一种用于手写体字符识别的非常高效的卷积神经网络。
• 卷积神经网络能够很好的利用图像的结构信息。
• 卷积层的参数较少，这也是由卷积层的主要特性即局部连接和共享权重所决定。
• 然而，LeNet模型就无法处理ImageNet这样比较大的图像数据集

 如何设计卷积神经网络的架构？

　　下面的正则表达式总结了一些经典的用于图片分类问题的卷积神经网络架构：

输入层   ——>  （卷积层 +   ——>  池化层 ？） +  ——>  全连接层  +

　　在上面的公式中，“卷积层  + ” 表示一层或者多层卷积层，大部分卷积神经网络中一般最多连续使用三层卷积层。 “池化层 ? ” 表示没有或者一层池化层。池化层虽然可以起到减少参数防止过拟合问题，但是在部分论文中可以直接通过调整卷积层步长来完成。所以有些卷积神经网络中没有池化层。在多轮卷积层和池化层之后，卷积神经网络在输出之前一般会经过1-2个全连接层。比如LeNet

 Inception-v3模型

　　上面学习了LeNet-5模型。这里学习inception结构以及 Inception-v3卷积神经网络模型。Inception结构是一种和LeNet-5结构完全不同的额卷积神经网络结构，在LeNet-5模型中，不同卷积层通过串联的方式连接在一起，而Inception-v3模型中的Inception结构是将不同的卷积层通过并联的方式结合在一起，下面学习inception结构，并通过Tensorflow-Slim工具来实现Inception-v3模型中的一个模块。

　　之前提到了一个卷积层可以使用边长为1,3或者5 的过滤器，那么如何在这些边长中选呢？Inception模块给出了一个方案，那就是同时使用所有不同尺寸的过滤器，然后再将得到的矩阵拼接起来。下图给出了inception模块的一个单元结构示意图：

　　　从图中可以看出，Inception模块首先使用不同尺寸的过滤器处理输入矩阵，在图中，最上方举证使用了边长为1的过滤器的卷积层前向传播的结果。类似的，中间矩阵使用的过滤器边长为1，下方矩阵使用的过滤器边长为5，不同的矩阵代表了Inception模块中的一条计算路径。虽然过滤器的大小不同，但如果所有的过滤器都使用全0填充且步长为1，那么前向传播得到的结果矩阵的长和宽都与输入矩阵一致。这样经过不同过滤器处理的结果矩阵可以拼接成一个更深的矩阵。如上图，可以将他们在深度这个维度上组合起来。

　　上图所示的Inception模块得到的结果矩阵的长和宽与输入一样，深度为红黄蓝三个矩阵深度的和。上图展示的是Inception模块的核心思想，真正在 Inception-v3模型中使用的Inception模块要更加复杂且多样。

　　下图给出Inception-3模型的架构图：

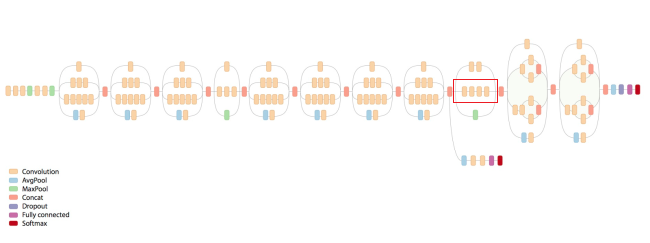
　　Inception-3模型总共有46层，由11个inception模块组成。上图标志出来的结构就是一个Inception模块，在Inception-3模型中有86个卷积层，如果将之前的程序搬过来，那么一个卷积就需要五行代码，于是总共需要480行代码来实现所有的卷积层，这样使得代码的可读性非常低。为了更好地实现类似Inception-3模块这样的复杂卷积神经网络，在下面将先学习TensorFlow-Slim 工具来更加简洁的实现一个卷积层，以下代码对比了直接使用TensorFlow实现一个卷积层和使用TensorFlow-Slim实现同样结构的神经网络的代码量。

# 直接使用TensorFlow原始API实现卷积层  with tf.variable_scope(scope_name):      weights = tf.get_variable("weights", ...)      biases = tf.get_variable('bias', ...)      conv = tf.nn.conv2d(...)  relu = tf.nn.relu(tf.nn.bias_add(conv, biases))    # 使用TensorFlow-Slim实现卷积层，通过TensorFlow-Slim可以在一行中实现一个卷积层的前向传播算法  # slim.conv2d 函数的有三个参数是必填的。第一个参数为输入节点矩阵  # 第二个参数是当前卷积层过滤器的深度，第三个参数是过滤器的尺寸  # 可选的参数有过滤器移动的步长，是否使用全0 填充，激活函数的选择以及变量的命名空间  net = slim.conv2d(input, 32, [3, 3])  

　　因为完整的Inception-v3 模型比较长，所以下面仅仅实现了一个Inception-v3模型中结构相对复杂的一个inception模块的代码实现：

#_*_coding:utf-8_*_  import tensorflow as tf    # slim.arg_scope 函数可以用于设置默认的参数取值  # 此函数第一个参数是一个函数列表，在这个列表中的函数将使用默认的参数取值  # 比如下面定义，调用 slim.conv2d(net, 320, [1, 1]) 函数会自动加上stride=1 和padding='SAME'参数  # 如果在函数调用时指定了stride。那么这里设置的默认值就不会再使用。通过这种方式可以减少冗余代码      with slim.arg_scope([slim.conv2d, slim.max_pool2d, slim.avg_pool2d],                      stride=1, padding='SAME'):      ...      # 此处省略了inception-v3模型中其他的网络结构而直接实现最后红框的inception结构      # 假设输入图片经过之前的神经网络前向传播的结果保存在变量net中      net = 上一层的输出节点矩阵      # 为一个inception模块声明一个统一的变量命名空间      with tf.variable_scope('Mixed_7c'):          # 给inception 模块中每一条路径声明一个命名空间          with tf.variable_scope('Branch_0'):              # 实现一个过滤器边长为1，深度为320的卷积层              branch_0 = slim.conv2d(net, 320, [1, 1], scope='Conv2d_0a_1x1')          # Inception 模块中第二条路径，这条计算路径上的结构本身也是一个Inception结构          with tf.variable_scope('Branch_1'):              branch_1 = slim.conv2d(net, 384, [1, 1], scope='Conv2d_0a_1x1')              # tf.concat 函数可以将多个矩阵拼接起来。tf.concat函数的第一个参数指定了拼接的维度              # 这里的3表示矩阵是在深度这个维度上及很小拼接              branch_1 = tf.concat(3, [                  # 此处2层卷积层的输入都是 branch_1 而不是 net                  slim.conv2d(branch_1, 384, [1, 3], scope='Conv2d_0b_1x3'),                  slim.conv2d(branch_1, 384, [3, 1], scope='Conv2d_0c_3x1')              ])            # Inception 模块中第三条路径 ，此计算路径也是一个inception结构          with tf.variable_scope('Branch_2'):              branch_2 = slim.conv2d(                  net, 448, [1, 1], scope='Conv2d_0a_1x1')              branch_2 = slim.conv2d(                  branch_2, 384, [3, 3], scope='Conv2d_0b_3x3')              branch_2 = tf.concat(3, [                  slim.conv2d(branch_2, 384, [1, 3], scope='Conv2d_0c_1x3'),                  slim.conv2d(branch_2, 384, [3, 1], scope='Conv2d_0d_3x1')              ])                    # Inception模块中的第四条路径          with tf.variable_scope("Branch_3"):              branch_3 = slim.avg_pool2d(                  net, [3, 3], scope='AvgPool_0a_3x3'              )              branch_3 = slim.avg_pool2d(                  branch_3, 192, [1, 1], scope='Conv2d_0b_1x1'              )                    # 当前Inception 模块的最后输出是由上面四个计算结果拼接得到的          net = tf.concat(3, [branch_0, branch_1, branch_2, branch_3])  

卷积神经网络迁移学习

　　下面学习迁移学习的概念以及如何通过TensorFlow来实现迁移学习。首先学习迁移学习的机制，并学习如何将一个数据集上训练好的卷积神经网络模型快速转义到另外一个数据集上，然后在给出一个具体的TensorFlow程序将ImageNet上训练好的inception-v3模型转移到另外一个图像分类数据集上。

迁移学习介绍

　　　之前介绍了1998年提出的LeNet-5 模型和2015年提出的Inception-v3模型，对比两个模型可以发现，卷积神经模型的层数和复杂度都发生了巨大的变化，下表给出了从2012年到2015年ILSVRC（Large Scale Visual Recognition Challenge）第一名模型的层数以及前五个答案的错误率。

　　从表中可以看到，随着模型层数及复杂度的增加，模型在ImageNet上的错误率也随着降低。然而，训练复杂的卷积神经网络需要非常多的标注数据。比如ImageNet图像分类数据集中有120万标注图片，所以才能将152层的ResNet的模型训练到大约96.5%的正确率。在真实的应用中，很难收集到如此多的标注数据。即使可以收集到，也需要花费大量人力物力。而且即使有海量的数据，要训练出一个复杂的卷积神经网络也需要几天甚至几周的时间。为了解决标注数据和训练时间的问题，可以使用迁移学习。

　　所谓迁移学习，就是将一个问题上训练好的模型通过简单的跳转使其适用于一个新的问题，下面将学习如何利用ImageNet数据集上训练好的Inception-v3模型来解决一个新的图像分类问题。根据论文（A Deep Convolutional Activation Feature for Generic Visual Recognition）的结论，可以保留训练好的Inception——v3模型中所有卷积层的参数，只是替换最后一层全连接层。在最后这一层全连接层之前的网络层称之为瓶颈处（bottleneck）。

　　将新的图像通过训练好的卷积神经网络直到瓶颈层的过程可以看成是对图像进行特征提取的过程。在训练好的Inception-v3模型中，因为将瓶颈层的输出再通过一个单层的全连接层神经网络可以很好地区分1000种类别的图像，所以有理由认为瓶颈层输出的节点向量可以被作为任何图像的一个更加精简且表达能力更强的特征向量。于是在新的数据集上，可以直接利用这个训练好的神经网络对图像进行特征提取，然后再将提取到的特征向量作为输入来训练一个新的单层全连接神经网络处理新的分类问题。

　　一般来说，在数据量足够的情况下，迁移学习的效果不如完全重新训练。但是迁移学习所需要的训练时间和训练样本要远远小于训练完整的模型。在没有GPU的普通台式电脑或者笔记本电脑上，下面给出的TensorFlow训练过程只需要大约五分钟，而且可以达到大概90%的正确率。

TensorFlow实现迁移学习

　　下面给出一个完整的Tensorflow程序来学习如何通过TensorFlow实现迁移学习。

 　　下载地址：http://download.tensorflow.org/example_images/flower_photos.tgz

　　inception-v3下载地址：https://storage.googleapis.com/download.tensorflow.org/models/inception_dec_2015.zip

　　解压之后的文件夹包含了5个子文件夹，每一个子文件夹的名称为一种花的名称，代表了不同的类别。平均每一种花有734张图片，每一张图片都是RGB色彩模型的，大小也不相同。和之前的样例不一样，在这里给出的程序将直接处理没有整理过的图像数据。同时，通过下面的命名可以下载谷歌提供的训练好的Inception-v3模型

 　　当新的数据集和已经训练好的模型都准备好之后，可以通过下面代码完成迁移学习的过程。

# _*_coding:utf-8_*_ import glob import os import random import numpy as np import tensorflow as tf from tensorflow.python.platform import gfile # Inception-v3模型瓶颈层的节点个数 BOTTLENECK_TENSOR_SIZE = 2048 # Inception-v3 模型中代表瓶颈层结果的张量名称 # 在谷歌提供的inception-v3模型中，这个张量名称就是‘pool_3/_reshape:0’ # 在训练的模型时，可以通过tensor.name来获取张量的名称 BOTTLENECK_TENSOR_NAME = 'pool_3/_reshape:0' # 图像输入张量所对应的名称 JEPG_DATA_TENSOR_NAME = 'DecodeJpeg/contents:0' # 下载的谷歌训练好的inception-v3模型文件名 MODEL_DIR = 'inception_dec_2015' # 下载的谷歌训练好的Inception-v3 模型文件名 MODEL_FILE = 'tensorflow_inception_graph.pb' # 因为一个训练数据会被使用多次，所以可以将原始图像通过inception-v3模型计算得到 # 的特征向量保存在文件中，免去重复的计算，下面的变量定义了这些文件的存放地址 CACHE_DIR = 'bottleneck1' if not os.path.exists(CACHE_DIR): os.mkdir(CACHE_DIR) # 图片数据文件夹，在这个文件夹中每一个子文件夹代表一个需要区分的类别 # 每个子文件夹中存放了对应类别的图片 INPUT_DATA = 'flower_photos' # 验证的数据百分比 VALIDATION_PERCENTAGE = 10 # 测试的数据百分比 TEST_PERCENTAGE = 10 # 定义神经网络的设置 LEARNING_RETE = 0.01 STEPS = 4000 BATCH = 100 def create_image_lists(testing_percentage, validation_percentage): ''' 这些函数从数据文件夹中所有的图片列表并按训练，验证，测试数据分开 :param testing_percentage: 测试数据集的大小 :param validation_percentage: 验证数据集的大小 :return: ''' # 得到的所有图片都存在result这个字典（dictionary）里 # 这个字典的key为类别的名称，value是也是一个字典，字典存储了所有的图片名称 result = {} # 获取当前目前下所有的子目录 INPUT_DATA 是数据文件夹的名称 sub_dirs = [x[0] for x in os.walk(INPUT_DATA)] # print(sub_dirs) #['flower_photos', 'flower_photos\daisy', 'flower_photos\dandelion', # 'flower_photos\roses', 'flower_photos\sunflowers', 'flower_photos\tulips'] # 得到的第一个目录是当前目录，不需要考虑 is_root_dir = True for sub_dir in sub_dirs: # 下面这个函数的作用就是去掉没有文件夹的目录 if is_root_dir: # print(is_root_dir) is_root_dir = False continue # 获取当前目录下所有的有效图片文件 extensions = ['jpg', 'jpeg', 'JPG', 'JPEG'] file_list = [] # os.path.basename(path) 返回path最后的文件名。如何path以／或结尾，那么就会返回空值。 # 即 os.path.split(path)的第二个元素 dir_name = os.path.basename(sub_dir) # # print(dir_name) # 各种花名的文件夹daisy dandelion roses sunflowers tulips for extension in extensions: # # 得出的path为 flower_photos/类别/*./照片类型 此时为绝对路径 file_glob = os.path.join(INPUT_DATA, dir_name, '*.' + extension) # # 返回所有匹配的文件路径列表 file_list.extend(glob.glob(file_glob)) # print(len(file_list)) # [1266, 1796, 1282, 1398, 1598] if not file_list: continue # 通过目录名获取类别的名称 label_name = dir_name.lower() # 初始化当前类别的训练数据集，测试数据集和验证数据集 training_images = [] testing_images = [] validation_images = [] for file_name in file_list: # print(file_name) # 'flower_photos\daisy\5794839_200acd910c_n.jpg', base_name = os.path.basename(file_name) # print(base_name) # 随机将数据分到训练数据集，测试数据集和验证数据集 chance = np.random.randint(100) if chance < validation_percentage: validation_images.append(base_name) elif chance < (testing_percentage + validation_percentage): testing_images.append(base_name) else: training_images.append(base_name) # 将当前类别的数据放入结果字典 result[label_name] = { 'dir': dir_name, 'training': training_images, 'testing': testing_images, 'validation': validation_images, } # 返回整理好的所有数据 # print(result.keys()) #(['daisy', 'dandelion', 'roses', 'sunflowers', 'tulips']) print(len(result.items())) print(len(result.keys())) return result def get_image_path(image_lists, image_dir, label_name, index, category): ''' 这个函数通过类别名称，所属数据集和图片编码获取一张图片的地址 :param image_lists: 给出了所有图片信息 :param image_dir:给出了根目录，存放图片数据的根目录和存放图片特征向量的根目录地址不同 :param label_name:给定了类别的名称 :param index:给定了需要获取的图片的编号 :param category:指定了需要获取的图片是在训练数据集，测试数据集还是验证数据 :return: ''' # 获取给定类别的所有图片的信息 label_lists = image_lists[label_name] # 根据所属数据集的名称获取集合中的全部图片信息 category_list = label_lists[category] mod_index = index % len(category_list) # 获取图片的文件名 base_name = category_list[mod_index] sub_dir = label_lists['dir'] # 最终地址为数据根目录的地址加上类别的文件夹加上图片的名称 full_path = os.path.join(image_dir, sub_dir, base_name) return full_path def get_bottleneck_path(image_lists, label_name, index, category): ''' 通过类别名称，所属数据集和图片编号获取经过Inception-v3模型处理之后的特征文件地址 :param image_lists: :param label_name: :param index: :param category: :return: ''' # return get_image_path(image_lists, CACHE_DIR, label_name, index, category) + '.txt' return get_image_path(image_lists, CACHE_DIR, label_name, index, category) # 这个函数使用加载的训练好的Inception-v3模型处理一张图片，得到这个图片的特征向量 def run_bottleneck_on_image(sess, image_data, image_data_tensor, bottleneck_tensor): # 这个过程实际上就是将当前图片作为输入计算瓶颈张量的值， # 这个瓶颈张量的值就是这张图片新的特征向量 bottleneck_values = sess.run(bottleneck_tensor, {image_data_tensor: image_data}) # 经过卷积神经网络处理的