箱形图和小提琴图
箱形图(Box-plot)
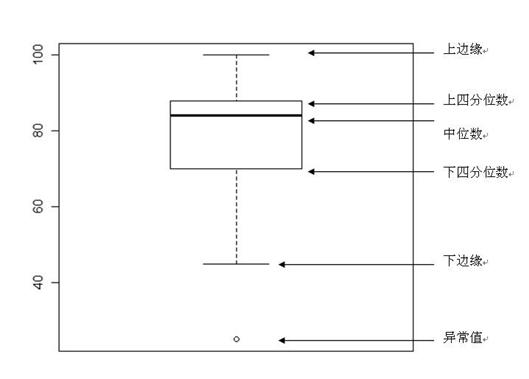
又称为盒须图、盒式图或箱线图,是一种用作显示一组数据分散情况资料的统计图,因形状如箱子而得名。它能显示出一组数据的最大值、最小值、中位数、及上下四分位数。
箱形图绘制须使用常用的统计量,能提供有关数据位置和分散情况的关键信息,尤其在比较不同的母体数据时更可表现其差异。
箱形图的绘制主要包含六个数据节点,需要先将数据从大到小进行排列,然后分别计算出它的上边缘,上四分位数,中位数,下四分位数,下边缘,还有一个异常值。
计算过程:
- 计算上四分位数(Q3),中位数,下四分位数(Q1)
- 计算上四分位数和下四分位数之间的差值,即四分位数差(IQR, interquartile range)Q3-Q1
- 绘制箱线图的上下范围,上限为上四分位数,下限为下四分位数。在箱子内部中位数的位置绘制横线。
- 大于上四分位数1.5倍四分位数差的值,或者小于下四分位数1.5倍四分位数差的值,划为异常值(outliers)。
- 异常值之外,最靠近上边缘和下边缘的两个值处,画横线,作为箱线图的触须。
- 极端异常值,即超出四分位数差3倍距离的异常值,用实心点表示;较为温和的异常值,即处于1.5倍-3倍四分位数差之间的异常值,用空心点表示。
- 为箱线图添加名称,数轴等
分位数
根据其将数列等分的形式不同可以分为中位数,四分位数,十分位数、百分位数等等。四分位数作为分位数的一种形式,在统计中有着十分重要的意义和作用。
四分位数(Quartile)也称四分位点,是指在统计学中把所有数值由小到大排列并分成四等份,处于三个分割点位置的数值。它是一组数据排序后处于25%和75%位置上的值。四分位数是通过3个点将全部数据等分为4部分,其中每部分包含25%的数据。很显然,中间的四分位数就是中位数,因此通常所说的四分位数是指处在25%位置上的数值(称为下四分位数)和处在75%位置上的数值(称为上四分位数)。与中位数的计算方法类似,根据未分组数据计算四分位数时,首先对数据进行排序,然后确定四分位数所在的位置,该位置上的数值就是四分位数。与中位数不同的是,四分位数位置的确定方法有几种,每种方法得到的结果会有一定差异,但差异不会很大。
四分位数有三个分位点,第一个四分位数就是通常所说的四分位数,称为下四分位数,第二个四分位数就是中位数,第三个四分位数称为上四分位数,分别用Q1、Q2、Q3表示。
- 第一四分位数 (Q1),又称“较小四分位数”,等于该样本中所有数值由小到大排列后第25%的数字。
- 第二四分位数 (Q2),又称“中位数”,等于该样本中所有数值由小到大排列后第50%的数字。
- 第三四分位数 (Q3),又称“较大四分位数”,等于该样本中所有数值由小到大排列后第75%的数字。
- 第三四分位数与第一四分位数的差距又称四分位距(InterQuartile Range,IQR)。
确定四分位数的位置的方法有多种,如
Q1位置 = (n+1) * 0.25
Q2位置 = (n+1) * 0.5
Q3位置 = (n+1) * 0.75
其中n表示项数
另一种确定方法
Q1位置 = 1 + (n-1) * 0.25
Q2位置 = 1 + (n-1) * 0.5
Q3位置 = 1 + (n-1) * 0.75
Demo
最简盒形图
import matplotlib.pyplot as plt import numpy as np all_data = [np.random.normal(0, std, 100) for std in range(1, 4)] fig = plt.figure(figsize=(8, 6)) plt.boxplot(all_data, notch=False, # box instead of notch shape sym='rs', # red squares for outliers vert=True) # vertical box aligmnent plt.xticks([y + 1 for y in range(len(all_data))], ['x1', 'x2', 'x3']) plt.xlabel('measurement x') t = plt.title('Box plot') plt.show() 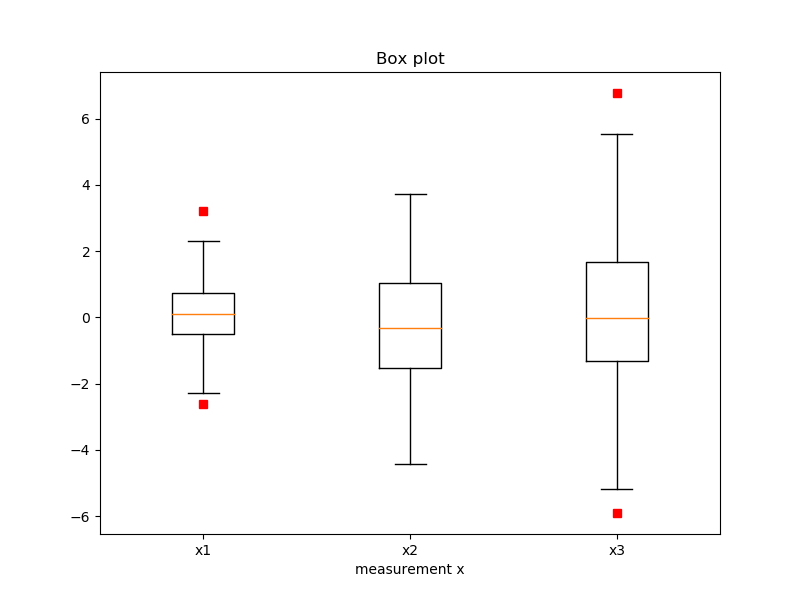
自定义颜色填充盒形图
import matplotlib.pyplot as plt import numpy as np all_data = [np.random.normal(0, std, 100) for std in range(1, 4)] fig = plt.figure(figsize=(8, 6)) bplot = plt.boxplot(all_data, notch=False, # notch shape vert=True, # vertical box aligmnent patch_artist=True) # fill with color colors = ['pink', 'lightblue', 'lightgreen'] for patch, color in zip(bplot['boxes'], colors): patch.set_facecolor(color) plt.xticks([y + 1 for y in range(len(all_data))], ['x1', 'x2', 'x3']) plt.xlabel('measurement x') t = plt.title('Box plot') plt.show()
小提琴图
小提琴图 (Violin Plot)是用来展示多组数据的分布状态以及概率密度。这种图表结合了箱形图和密度图的特征,主要用来显示数据的分布形状。跟箱形图类似,但是在密度层面展示更好。在数据量非常大不方便一个一个展示的时候小提琴图特别适用。
小提琴图概念图

Demo
import matplotlib.pyplot as plt import numpy as np fig, axes = plt.subplots(figsize=(12, 5)) all_data = [np.random.normal(0, std, 100) for std in range(6, 10)] axes.violinplot(all_data, showmeans=False, showmedians=True ) axes.set_title('violin plot') # adding horizontal grid lines axes.yaxis.grid(True) axes.set_xticks([y + 1 for y in range(len(all_data))], ) axes.set_xlabel('xlabel') axes.set_ylabel('ylabel') plt.setp(axes, xticks=[y + 1 for y in range(len(all_data))], xticklabels=['x1', 'x2', 'x3', 'x4'], ) plt.show()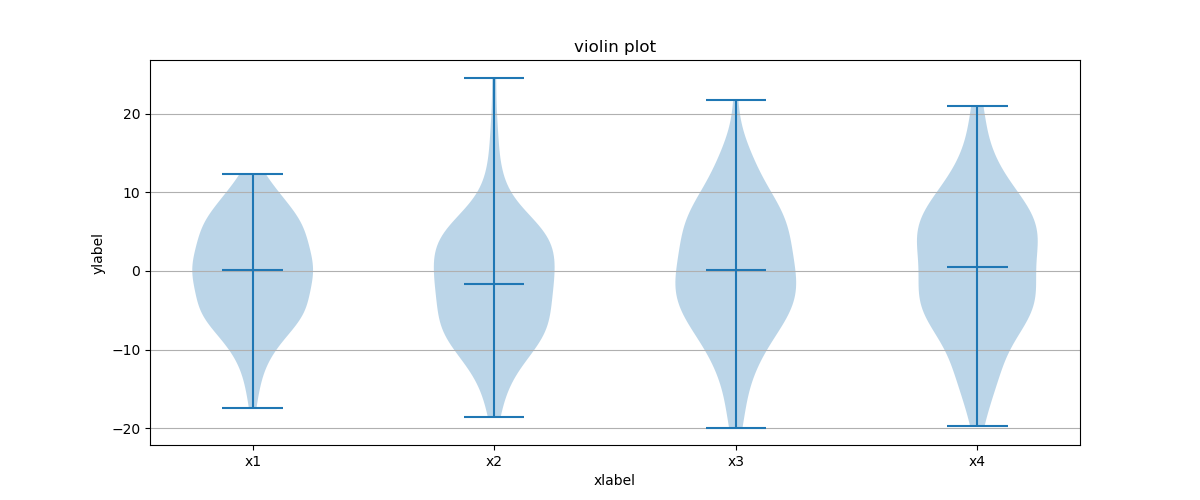
参考文献
百度百科-四分位数
python绘制盒状图和小提琴图
箱形图绘制-水平,并列等
箱形图与小提琴图概念介绍
seaborn小提琴图
您可能感兴趣的文章
- 【Keras】Keras入门指南
- PCA(主成分分析)python实现
- 第六次人口普查数据分析
- 第六次人口普查数据分析
- 第六次人口普查数据分析
- 阴谋还是悲剧?- 基于机器学习假设检验视角,看泰坦尼克号事件
- 基于Spring Boot + Dubbo的全链路日志追踪(二) – 明天以后
- vue组件引入本地静态图片 – 牧云橙的个人空间
未经允许不得转载:杂烩网 » 箱形图和小提琴图




